|
| |
Combinations
Sometimes, in order to factorise an expression as fully as possible,
you need a combination of quadratic factorisation with the taking out of other common
factors.
| Example
10 |
|
|
2x2(x + 1) - 4x |
Strategy |
2x is in common.
2x2(x + 1)
- 4x
= 2x(x(x + 1) - 2(2x))
= 2x(x(x + 1) - 2)
= 2x(x2 + x - 2) |
Factorise by taking out common factors first.
Try to simplify the expression in the brackets. If it is a quadratic expression,
try to factorise it. |
| For x2
+ x - 2, A = 1, B = 1, C = -2 |
Obtain the values of A, B and
C by inspection |

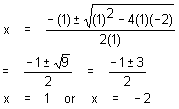
Hence x2 + x - 2
= (x - 1)(x + 2)
|
Substitute the values into
the quadratic formula and simplify.
To make the factorisation correct we have to multiply by the coefficient
of x2 in the original quadratic, that is multiply by A. (No action
is required if A = 1.) |
2x2(x + 1) - 4x = 2x(x - 1)(x + 2) |
Put it all together. |
Now try your hand at some really tough examples!
Exercise
10
Factorise each expression as far as possible. |
| |
<< Quadratic Functions Factoriser | Factorisation
Index |
|

