Concave
Up, Concave Down, Points of Inflection
We have seen previously that the sign of the derivative provides
us with information about where a function (and its graph) is increasing,
decreasing or stationary. We now look at the "direction
of bending" of a graph, i.e. whether the graph is "concave
up" or "concave down".
A graph is said to be concave
up at a point if the tangent line to the graph
at that point lies below the graph in the vicinity of the point
and concave down
at a point if the tangent line lies above the graph in the
vicinity of the point.
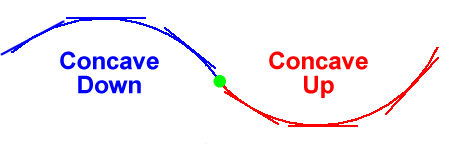
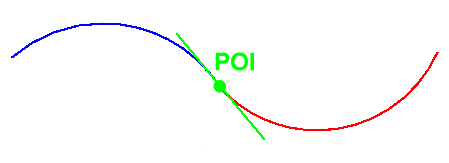
A point where the concavity changes (from up to down or down to
up) is called a point of inflection
(POI); note that the
tangent line to a graph at a point of inflection must cross the
graph at that point.
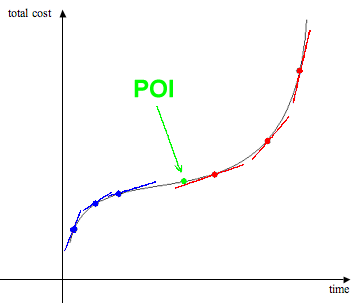
Now let's look at concavity from a slightly different perspective.
Consider the graph of a cost function shown below. The graph shows
that the total cost of a certain activity increases sharply at the
beginning and then rises more and more slowly until a point when
the total cost begins to rise more sharply again. The blue colour
indicates a region where the slope of the tangent decreases. That
is, in this region the rate at which the cost function increases,
decreases. The red colour indicates a region where the slope of
the tangent increases, i.e. the rate at which the cost function
increases also increases. By our previous definitions, the blue
area is concave downward and the red area is concave upwards. The
green point is the point at which the rate of change of the
slope changes from decreasing to increasing. It is also the
point at which the concavity of the function changes from downward
to upward. This point is called a point of inflection (POI).
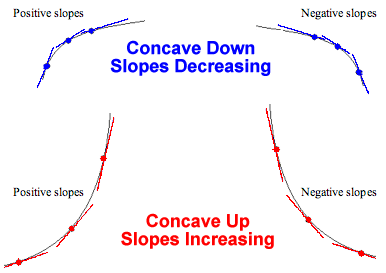
In general, note that regardless of the sign of the
slope (positive, negative or zero), the slopes of the tangent are
decreasing as we move from left to right when the graph is concave
down and increasing (from left to right) when it is concave up.
Exercise
Look at the applet below. Note that the function is shown in the top line,
the function's graph on the left and it's derivative's graph on the right. Use
the slider to change the value of x. Convince
yourself that the graph of the given function f is concave up where
the derivative f ' (the slope of the tangent) is an increasing function,
and concave down where the derivative f ' is a decreasing function.
Examine the fourteen examples provided in the scroll bar on the top of the
applet or enter your own function in the space below the graphs and press new
function to display the graphs. To enter your own function, you must use the
symbols + for add, − for
subtract, * for multiply, / for divide, and ^ to raise to a power. You
can also use various mathematical functions: sin, cos, tan, sec, cot, csc, arcsin,
arccos, arctan, exp, ln, log2, log10, abs, sqrt and cubert. (Here, "abs"
is the absolute value function, "sqrt" is the square root function
and
"cubert" is the cube root function.)
Continue until you are convinced that, in all cases, the graph
of the given function f is concave up where the derivative f '
(the slope of the tangent) is an increasing function, and concave down where the
derivative f ' is a decreasing function.
| Make sure you understand
the following connections between the two graphs.
- When the function y = f (x) is concave up, the graph of its derivative y = f '(x) is increasing.
- When the function y = f (x) is concave down, the graph of its derivative y = f '(x) is decreasing.
- When the function y = f (x) has a point of inflection (changes from concave up to concave down), the graph of its derivative y = f '(x) has a maximum or minimum (and so changes from increasing to decreasing or decreasing to increasing respectively).
|
|
Can't see the above java applet? Click here
to see how to enable Java on your web browser. (This applet
is based on free Java applets from JavaMath
)
Given the above, we can decide whether a function is increasing
or decreasing by looking at the sign of its derivative. To decide
whether f ' is increasing or decreasing, we must look at
the sign of its derivative (the derivative of f '). This
derivative of f ' (i.e. the derivative of the derivative
of f) is called the second derivative
of f and is denoted by f ''.
In terms of the second derivative, we can summarize our earlier
discussion as follows
- The graph of y = f (x) is concave upward on those intervals where y = f "(x) > 0.
- The graph of y = f (x) is concave downward on those intervals where y = f "(x) < 0.
- If the graph of y = f (x) has a point of inflection then y = f "(x) = 0.
Exercise
Examine the first example given below. Note that the function is shown on
the left, the first derivative in the middle and the second derivative on the
left.
Test that the three properties noted just above are true.
Examine the fourteen examples provided in the scroll bar on the top of the
applet below or enter your own function in the box provided. If you enter your
own function, you must use the symbols + for add, −
for subtract, * for multiply, / for divide, and ^ to raise to a power. You
can also use various mathematical functions: sin, cos, tan, sec, cot, csc, arcsin,
arccos, arctan, exp, ln, log2, log10, abs, sqrt and cubert. (Here, "abs"
is the absolute value function, "sqrt" is the square root function and
"cubert" is the cube root function.)
| Make sure you understand
the following connections between the two graphs.
- The graph of y = f (x) is concave upward on those intervals where y = f "(x) > 0.
- The graph of y = f (x) is concave downward on those intervals where y = f "(x) < 0.
- If the graph of y = f (x) has a point of inflection then y = f "(x) = 0.
|
|
Can't see the above java applet? Click here
to see how to enable Java on your web browser. (This applet is based
on free Java applets from JavaMath
)
We can calculate the second derivative to determine the concavity
of the function's curve at any point.
- Calculate the second derivative.
- Substitute the value of x.
- If f "(x) > 0, the graph is concave
upward at that value of x.
- If f "(x) = 0, the graph may have
a point of inflection at that value of x. To check, consider
the value of f "(x) at values of x to
either side of the point of interest.
- If f "(x) < 0, the graph is concave
downward at that value of x.
Example
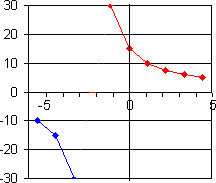 What is the shape of the graph of What is the shape of the graph of 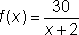 at x =
0? at x =
0?
Calculate f "(x).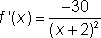 and and 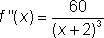
When x = 0, 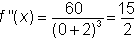
f"(x) > 0, so the graph is concave
upward at x = 0. In fact f "(x) > 0 for all x > -2 so the graph is concave upward in that range. f "(x) < 0 for all x < -2 so the graph is concave downward if x < -2.
By contrast, consider h(x) = 6, which we know has a horizontal line graph. At all points h '(x) = 0 and h "(x) = 0 but there is no point of inflection.
Exercise
Similarly, we can find the points of inflection on a function's
graph by calculation.
- Calculate the second derivative.
- Solve the equation f "(x) = 0 to
obtain the value(s) of x at the possible point(s) of inflection.
Check the f "(x) value to either side
of each x value to be sure each gives a point of inflection.
- Substitute the value(s) of x into f(x).
- Hence deduce the coordinates of the point(s) of inflection.
Example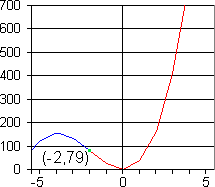 If f(x) = 5x3 + 30x2 + x + 1 If f(x) = 5x3 + 30x2 + x + 1
then f '(x) = 15x2 + 60x + 1
and f ''(x) = 30x + 60.
At points of inflection, f "(x) = 0. This is true when 0 = 30x + 60, that is x = -2.
f(-2) = 5(-2)3 + 30(-2)2 +
(-2) + 1 = 79
Below x = -2, the value of
the second derivative, 30x + 60, will be
negative so the curve is concave down. For higher values of x,
the value of the second derivative, 30x + 60,
will be positive so the curve is concave up. We can conclude that the point (-2,79) is
a point of inflection.
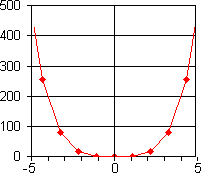 Consider f(x) = x4. Consider f(x) = x4.
Solving f "(x) = 12x2 =
0 yields x = 0. At values of x < 0,
the second derivative is positive. At values of x > 0,
the second derivative is positive. (0,0) is a local minimum.
Exercise
|

