The product rule states:

By the definition of the derivative

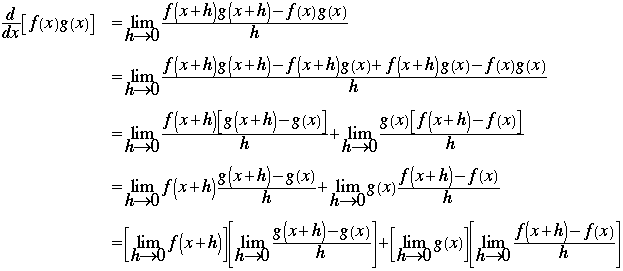
By the definition of the derivative

                     

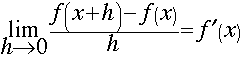
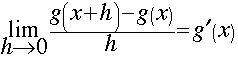
f is differentiable at x and therefore continuous at x. Hence

The limit of a constant is the value of the constant. As there is no h in g(x), we can treat g(x) as a constant when finding its limit as h tends to zero. So

                     

Using each of the above facts we then obtain:

which is the product rule.

Back to The Product Rule