- y = ln cos 5x
- y = 1 − x3e−9x
- y =
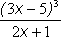
- y =
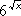
- y = (1 + 2x)(3 − 4x)(5 + 6x)
This problem is a composite function of a composite function so use the Chain Rule twice.
 =
= ![]()
![]() (cos 5x) using the Chain Rule
(cos 5x) using the Chain Rule
 =
= ![]() (−sin 5x)
(−sin 5x)![]() 5x using the Chain Rule
5x using the Chain Rule
 =
= ![]() (−sin 5x)(5) using basic derivatives
(−sin 5x)(5) using basic derivatives
 = −5tan 5x simplifying
= −5tan 5x simplifying
This problem simplifies to differentiating a product of a basic function and a composite function, so use the Product Rule then the Chain Rule.
 = e−9x
= e−9x![]() (−x3) + (−x3)
(−x3) + (−x3) ![]() e−9x using the Product Rule
e−9x using the Product Rule
 = e−9x
= e−9x![]() (−x3) + (−x3) e−9x
(−x3) + (−x3) e−9x![]() (−9x) using the Chain Rule on the right hand expression
(−9x) using the Chain Rule on the right hand expression
 = e−9x(−3x2) + (−x3) e−9x (−9) using basic derivatives
= e−9x(−3x2) + (−x3) e−9x (−9) using basic derivatives
 = (9x3 − 3x2) e−9x tidying up
= (9x3 − 3x2) e−9x tidying up
This problem is a quotient of a composite function and a polynomial so the Quotient Rule and Chain Rule should be used.
 =
= 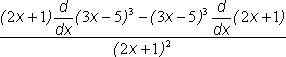 using the Quotient Rule
using the Quotient Rule
 =
= 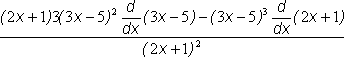 using the Chain Rule on the left expression
using the Chain Rule on the left expression
 =
= ![]() using basic derivatives
using basic derivatives
 =
= ![]() simplifying
simplifying
 =
= ![]() taking out the common factor of (3x − 5)2
taking out the common factor of (3x − 5)2
 =
= ![]() multiplying out the right hand brackets
multiplying out the right hand brackets
 =
= ![]() collecting like terms
collecting like terms
This problem is a variable power function so take the natural logarithm first then differentiateusing the Chain Rule.
ln y = ![]() (ln 6) taking logs
(ln 6) taking logs
![]()
 = ½x−½(ln 6) differentiating
= ½x−½(ln 6) differentiating
 = ½yx−½(ln 6) multiplying both sides by y
= ½yx−½(ln 6) multiplying both sides by y
 =
= ![]() substituting for y and expressing as a fraction
substituting for y and expressing as a fraction
This problem is a product of 3 polynomials. You can either use algebraic manipulation to expand the brackets to obtain one cubic polynomial then differentiate or you can use the Product Rule twice if you like a lot of work.
Either
y = (1 + 2x)(3 − 4x)(5 + 6x) = (3 + 6 x − 8x − 8x2)(5 + 6x) = (3 + 2x − 8x2)(5 + 6x)
y = 15 + 18x + 10x + 12x2 − 40x2 − 48x3 = 15 + 28x − 28x2 − 48x3 expanding the brackets
 = 28 − 56x − 144x2
= 28 − 56x − 144x2
Or
 = (5 + 6x)
= (5 + 6x)![]() (1 + 2x)(3 − 4x) + (1 + 2x)(3 − 4x)
(1 + 2x)(3 − 4x) + (1 + 2x)(3 − 4x)![]() (5 + 6x) applying the Product Rule
(5 + 6x) applying the Product Rule
 = (5 + 6x)((3 − 4x)
= (5 + 6x)((3 − 4x)![]() (1 + 2x) + (1 + 2x)
(1 + 2x) + (1 + 2x)![]() (3 − 4x)) + (1 + 2x)(3 − 4x)
(3 − 4x)) + (1 + 2x)(3 − 4x)![]() (5 + 6x) applying the Product Rule to the left expression
(5 + 6x) applying the Product Rule to the left expression
 = (5 + 6x)((3 − 4x) (2) + (1 + 2x)(−4)) + (1 + 2x)(3 − 4x)(6) using basic derivatives
= (5 + 6x)((3 − 4x) (2) + (1 + 2x)(−4)) + (1 + 2x)(3 − 4x)(6) using basic derivatives
 = (5 + 6x)(6 − 8x − 4 − 8x) + 6(1 + 2x)(3 − 4x) expanding brackets on the left
= (5 + 6x)(6 − 8x − 4 − 8x) + 6(1 + 2x)(3 − 4x) expanding brackets on the left
 = (5 + 6x)(2 − 16 x) + 6(1 + 2x)(3 − 4x) collecting like terms on the left
= (5 + 6x)(2 − 16 x) + 6(1 + 2x)(3 − 4x) collecting like terms on the left
 = (10 + 12x − 80x − 96x2) + 6(3 − 4x + 6x − 8x2) expanding brackets
= (10 + 12x − 80x − 96x2) + 6(3 − 4x + 6x − 8x2) expanding brackets
 = (10 − 68x − 96x2) + 6(3 + 2x − 8x2) collecting like terms
= (10 − 68x − 96x2) + 6(3 + 2x − 8x2) collecting like terms
 = (10 − 68x − 96x2) + (18 + 12x − 48x2) expanding bracket
= (10 − 68x − 96x2) + (18 + 12x − 48x2) expanding bracket
 = 28 − 56 x − 144x2 collecting like terms
= 28 − 56 x − 144x2 collecting like terms